Home About
Negative Dimensions

Making Sense of Negative Dimensions

Idea

How do we make sense of negative dimensions?

Background

$$\newcommand{\N}[0]{\mathbb{N}} \newcommand{\Z}[0]{\mathbb{Z}} \newcommand{\Q}[0]{\mathbb{Q}} \newcommand{\R}[0]{\mathbb{R}}$$ There is an anonymous quote that occasionally surfaces in higher mathematics along the lines of

"Once mathematicians start counting, they never stop."

Loosely speaking, it concerns the tendency of mathematicians to generalize structures to $n$-structures. This has proved very successful in a number of areas of mathematics. In fact, there exists a comprehensive online encyclopedia of many places in mathematics that this archetype arises, aptly called nLab. Just as with the evolution of human understanding of number systems, so too we find an even greater pattern in the evolution of the generalization of many structures, along the path of $$\{0\}\mapsto\N\mapsto\Z\mapsto\Q\mapsto\R\mapsto\cdots$$ Hence, the step from structures to $n$-structures is often only the beginning. After we begin some sort of induction, we may then ask about going in the reverse direction, viz. into the negatives. This concept, called negative thinking, according to nLab,

"is a way of thinking about categorification by considering what the original concept is a categorification of. That is, to better understand how [structures] are categorified to become [2-structures], [3-structures], and so on, you think about how structures are themselves a categorification of [0-structures], [(-1)-structures], and so on. Generally, the concept of [n-structure] stops making sense for small values of n after a few steps, but it does make sense surprisingly often for at least some non-positive values. [...] More generally, [this concept] can apply whenever you have a sequence of mathematical objects and ask yourself what came before the beginning?"

But not all beginnings afford an easy journey. In particular, although it has been long-established that, not only is our algebra well-equipped to study geometry in $1$, $2$, and $3$-dimensions, but is also perfectly capable of describing $n$-dimensions for any $n\in\N$, we seem to hit an impassible singularity at $n=0$, with nothing but echoes of what structures lay beyond $n<0$. The concern of this article is to shed light on this mystery. That is to say, we look at how generalizing our understanding to negative dimensions thwarts most attempts, and despite this, why there might be good reason for studying such. At worst, this article symbolizes the impossibility of negative dimensions; and at best, a collection of facts about what exists within them.

Initial observations

Based on our understanding of non-negative dimensions, we may start collecting some questions about the expected behavior of negative dimensions.

Regular n-polytopes

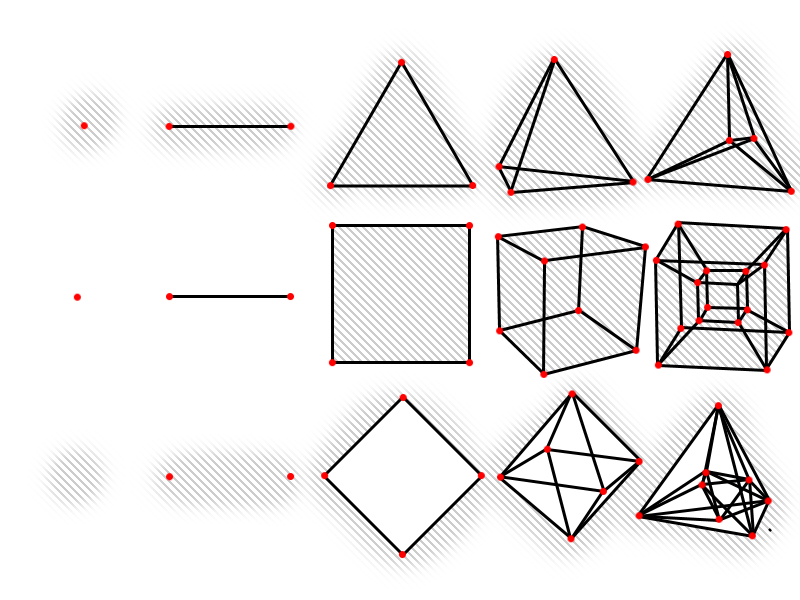
regular polytopes

$$\text{Figure 1. Wire-frame projections of $n$-simplices, $n$-cubes, and $n$-orthoplices for $0\leq n \leq 5$}.$$ We may begin exploring what structures exist in negative dimensions by taking some family of shapes, which we know exist in $n\in\N$ dimensions, then simply observe the behaviour of their equations for $n<0$. A nice initial choice are the three families of regular polytopes, which are the $n$-cubes, $n$-simplices, and $n$-otherplices. Each of these families have simple equations for the number of vertices, edges, faces ($k=0,1,2$), etc, based on binomial coefficients. The number of $k$-cells in an $n$-simplex, $n$-cube, and $n$-orthoplex, are respectively $$S(n,k)={{n+1}\choose{k+1}}\text{, }C(n,k)= 2^{n-k}{n \choose k}\text{, and }O(n,k)=2^{k+1}{n \choose {k + 1}}.$$
$$\text{Graph 1. Interactive graphs of $S(n,k)$, $C(n,k)$, and $O(n,k)$ for a fixed $n$.}$$ Unlike other instances in mathematics where formulae spit out, say, an $\infty$, become discontinuous, or are otherwise undefined, to indicate a lack of reason to suspect a meaningful value for a given input, these formulae do none of those things for negative values. In fact, they're perfectly defined both for $n<0$ and $k<0$. Hence, they are excellent candidates to study what problems we may face when generalizing structures to negative dimensions. There are really $4^2=16$ cases to consider, which correspond to when the dimensions of $n$ or $k$ are positive, negative, zero and $-1$. The reason for $-1$ having its own case is an interesting discussion, which we save for a later section. With this is mind, we look at what values, $S, C$ and $O$ take on in all 16 cases. $$\begin{array}{ c | c | c | c | c | } & k < -1 & k = -1 & k = 0 & k > 0 \\ \hline n < -1 & \Z & \{0\} & \Q\cap (0, 1) & \Q_{\neq 0}\cap (-1, 1)\\ \hline n = -1 & \Z_{\neq 0} & \{0\} & \left\{\frac{1}{2}\right\} & \Q_{>0}^{<1}\\ \hline n = 0 & \{0\} & \{0\} & \{1\} & \{0\}\\ \hline n > 0 & \{0\} & \{0\} & \Z^+ & \N\\ \hline \end{array}$$ $$\text{Table 1. Classes of values taken on by $C(n,k)$ in various cases.}$$ $$\begin{array}{ c | c | c | c | c | } & k < -1 & k = -1 & k = 0 & k > 0 \\ \hline n < -1 & \Z & \{1\} & \Z^- & \Z_{\neq 0}\\ \hline n = -1 & \{0\} & \{1\} & \{0\} & \{0\}\\ \hline n = 0 & \{0\} & \{1\} & \{1\} & \{0\}\\ \hline n > 0 & \{0\} & \{1\} & \Z^+ & \N\\ \hline \end{array}$$ $$\text{Table 2. Classes of values taken on by $S(n,k)$ in various cases.}$$ $$\begin{array}{ c | c | c | c | c | } & k < -1 & k = -1 & k = 0 & k > 0 \\ \hline n < -1 & \Q_{\neq0}\cap (-1:1) & \{0\} & \Z^- & \Z_{\neq 0}\\ \hline n = -1 & \Q_{\neq0}\cap (-1:1) & \{1\} & \{-2\} & \Z_{\neq 0}\\ \hline n = 0 & 0 & \{1\} & \{0\} & \{0\}\\ \hline n > 0 & 0 & \{1\} & \Z^+ & \N\\ \hline \end{array}$$ $$\text{Table 3. Classes of values taken on by $O(n,k)$ in various cases.}$$ There are really only two things preventing us from fully making sense of the whole table of these tables, which is how to make sense of $n$-cells decomposing into a negative and / or fractional amount of $k$-cells. Fortunately, we may still make some sense of some special cases. For example, row 1 of Table 1 tells us that any positive-dimensional cube cannot be deconstructed into any negative-dimensional components, but can be into positive integer number of vertices, and a natural number of other positive-dimensional components. Furthermore,

(-1)-cells as negative space

The second column of Table 2 indicates that a simplex of any dimension contains a singular $(-1)$-cell. This, in particular, is an interesting result, for it reveals that some positive-dimensional shapes may have negative-dimensional components, so we may not have to look further than the shapes we are already familiar with to yield some hints. For instance, according to $S(2,-1)=1$, a humble triangle (2-simplex) is comprised of a singular $(-1)$-cell. Exactly what part of it this corresponds to is a bit of a mystery, but it is worth considering.
In addition to these formulae being defined for negative values, there are two good reason to suspect that these values are not extraneous. The first is, less formally, the simplicity of them. To argue for other values would require modifying them in some non-trivial way. Secondly, more formally, duality. Given the fact that $n$-cubes are dual to $n$-orthoplices, and that $n$-simplices are dual to themselves, we expect the symmetries $$\begin{align*} C\left(\frac{n-1}{2}-x,k\right) &= O\left(\frac{n-1}{2}+x,k\right), \\ S\left(\frac{n-1}{2}-x,k\right) &= S\left(\frac{n-1}{2}+x,k\right). \end{align*}$$ For example, in the case of $n=3$, we find that edges are dual to edges, faces are dual to vertices, but also that cells are dual to $(-1)$-cells. Hence, if we are to assume that $n$-simplices and $n$-cubes are composed of one $n$-cell, then we should expect $n$-simplices and $n$-orthoplices to contain one $(-1)$-cell. Interestingly however, this also implies that $n$-orthoplices are \textit{not} composed of any $n$-cells. This is peculiar because it is traditionally assumed that all $n$-polytopes are comprised of one $n$-cell, namely their own volume. However, in the case of 2D, we claim this is not so unusual. It is already well known that the faces and vertices of graphs are dual to eachother, and the exterior region of a graph is considered a face / vertex in its dual. Therefore, we conjecture that $(-1)$-cells can be thought of as the negative space around the shape, as is illustrated in Figure 1 by the thatched lines.
Under this interpretation we may realize that, canonically it would seem, $n$-cubes have only an interior, $n$-orthoplices have only an exterior, and $n$-simplices are expansive in all directions. [1][1] As a rather bizarre historical coincidence, there is a natural correspondence to the ancient interpretation of the platonic solids; 3-cubes representing earth, 3-orthoplicies (octohedra) representing air, and 3-simplices (tetrahedra) representing fire.
This also provides a reason why the 1-simplex, 1-cube, and 1-orthoplex are all different shapes (also 0-cube, 0-simplex, and 0-orthoplex). For example, a 0-simplex is a point with negative space, a 0-cube is just a point, and a 0-orthoplex is just negative space.

Euler characteristic

We must nevertheless be careful, however, to respect the Euler characteristic. If we extend the definition in the most natural way, we find the Euler characteristics of the $n$-cube, $n$-simplex, and $n$-orthoplex to be $$\begin{align*} \chi_{C}(n) &= \sum_{k\in \Z}C(n,k) = 1,\\ \chi_{S}(n) &= \sum_{k\in \Z}S(n,k) = 0,\\ \chi_{O}(n) &= \sum_{k\in \Z}O(n,k) = -(-1)^n, \end{align*}$$ respectively.

k-cubes meeting along j-cubes

Another interesting case within these tables which still provide some intuition are in the case of $n$-cubes. For one, all $k$-cells of an $n$-cube are $k$-cubes themselves. We may notice that a negative-dimensional cube may be deconstructed into a positive integer number of other negative-dimensional-cubes, when $n\equiv k\mod 2$ and $k\leq n$. For instance, $(-1)$-cube may be deconstructed into $4$ $(-3)$-cubes, a $(-3)$-cube is comprised of $24$ $(-5)$-cubes. However, a $(-1)$-cube itself is made up of $16$ $(-5)$-cubes, not $4\cdot24=96$. This makes sense, because although a regular cube, for another example, is comprised of 6 faces, and each face has 4 edges, a cube has 12 edges and not $6\cdot 4=24$. This is important to mention, because it tells us about its structure. For instance, the fact that the 24 edges of 6 faces reduces to 12 when forming a cube, reveals that the number of faces meeting at an edge is $\frac{24}{12}=2$. Therefore, by the same logic, since we have 96 $(-5)$-cubes of 4 $(-3)$-cubes reducing to 16 in composition of a $(-1)$-cube, this reveals that the number of $(-3)$-cubes meeting along a $(-5)$-cube is $\frac{96}{16}=6$. In general, in an $n$-cube, the number of $k$-cubes meeting along a $j$-cube is given by $$M_C(n,k,j)=\frac{C(n, k)C(j,k)}{C(n, j)}=\frac{{n \choose k}{k \choose j}}{{n \choose j}}=\frac{(n-j)!}{(n-k)!(k-j)!}.$$

n-spheres

Another simple class of shapes existing in $n$-dimensions are the $n$-spheres. With the standard Euclidean norm and radius $R$, they have $n$-volumes and $n$-surface-areas defined by $$V_n=\frac{\pi^{\frac{n}{2}}}{\Gamma\left(\frac{n}{2}+1\right)}R^n\text{ and }S_n=\frac{2\pi^{\frac{n}{2}}}{\Gamma\left(\frac{n}{2}\right)}R^{n-1}.$$
$$\text{Graph 2. Interactive graphs of $V_n$ and $S_n$ for a fixed $R$.}$$ Since the gamma function has simple poles at non-positive integers, we find that $n$-spheres must have zero $n$-volume and $n$-surface-area for $n\in\{-2,-4,-6,\dots\}$. However, other negative-dimensional-spheres for $n=\{-1,-3,-5,\dots\}$ are less trivial. For instance, the $(-1)$-sphere would appear to have a $(-1)$-volume and $(-1)$-surface area of $$V_{-1}=\frac{1}{\pi r}\text{ and }S_{-1}=-\frac{1}{\pi r^2}.$$ It is not so difficult to show that the $n$-volume and $n$-surface-area of negative dimensional spheres have opposite signs of each other. However this does leave open the question of what negative values of these measures mean.

Set-theoretical problems

One of the more canonical approaches to studying negative dimensions is through set theory. We may remember that the definition of $A^B$ is defined as the set of all functions from $B$ to $A$. For example, a coordinate $(x, y)\in\R^2$ is, strictly speaking, a function $(x, y):\{0, 1\}\mapsto \mathbb{R}$ s.t. $(x,y)(0)=x$ and $(x, y)(1)=y$, since $2:=\{0,1\}$ as a Von Neumann ordinal. So, the problem of studying $\R^n$ for negative $n$ reduces to finding a suitable definition while dropping the least relevant properties. Unfortunately, we must inevitably drop several important ones. For all $m,n\in\N$, Notice, however, that these problems really only arise from questioning how to connect the negatives to $0$. That is to say, it is possible to define a set of negatives where $m+n\cong m\sqcup n$ and $m\le n\iff m\subseteq n$ for any $m,n\in\Z^-$, however we would have to perform some surgery to these definitions of addition and order to bridge the gap with the naturals.
Furthermore, natural numbers are considered equivalent up to equivalence of cardinality. Hence, without relaxing this condition, any suitable choice for the negatives must not only have infinite cardinality, but all be uncountable except for at most one, in order to be distinct from the naturals and from eachother. That is, unless we find a suitable definition for negative cardinality.

A p-adic inspired proposal for negative ordinals

We propose one definition for negative ordinals, inspired by $p$-adics. We will first give a brief overview of them and outline several ways in which they are already natural extensions to non-negative integers, before extending this notion set-theoretically.

Motivation

Informally, instead of signs (e.g; $+$ or $-$), and expansions to the right of the radix point, $p$-adic numbers can be thought of as what would happen if we extended natural numbers to allow for infinite digits to the left of the radix point. It turns out, many $p$-adic expansions behave similarly to negative integers, rationals, and even real and complex numbers, under usual notions of arithmetic. For instance, in the $2$-adics[2][2] The $p$ in $p$-adic plays the role of a base., we have $$\dots1111111_2=-1,$$ where the left-hand-side denotes the 2-adic expansion of the right-hand-side. Technically, we are mixing two different systems here, for in the 2-adics the right-hand-side is what would be represnted by the left, but hopefully the idea comes across, anyway, that $\dots1111111_2$ denotes a number $x$ s.t. $x+1=0$.
The $p$-adics have surprisingly deep connections to many areas of math, and are arguably just as natural as traditional number systems, albeit unintuitive as they may seem. To highlight this, we give 5 examples of how they may "show up" naturally. Attempting to perform arithmetic with $\dots1111111_2$, interpreted solely as we would any other natural binary number, yields something which behaves identically to $-1$ in many ways. Finally, it is not just the 2-adics expansions, let alone for $-1$, which obey these natural properties. With these observations, we are sure that anyone with enough experience with them would also argue (or at least understand the argument) that they are more than just a notational "hack", but are truly representative of negative (and rational, etc) quantities which we are already familiar with; we just have to let go of our attachment to the traditional notational systems we are immersed in.

Definition

A keen observer may notice that, in set theory, positional notation isn't even a concept. Sets are unordered, by definition, hence they have no notion of digits. If anything, they are unary, for a number is equivalent only to its cardinality. Nonetheless, there is still one concept of $p$-adics that may analagously carry over in set theory.
Notice that, a natural number has only finitely many non-zero digits to the left of its radix point, whereas a negative integer has infinite. Even more to the point, the more non-zero digits a natural number has, the greater it is, generally; meanwhile, the more zero digits a negative number has, the greater (its absolute value) is[3][3] As an interesting aside, if a $p$-adic number has finite non-zero or zero-digits iff. it is an intenger.. So in a somewhat informal, yet somehow intuitive, sense, in the $p$-adics, the negatives and positives form something of a closed loop (similar to the Riemann sphere). More formally, negatives are a limit of sequences of the positives, and $0$ is a limit of a sequence of negatives. For example, the sequence $1_2=1$, $11_2=3$, $111_2=7$, etc., despite becoming more and more positive (i.e; less and less negative), approaches $\dots11111111_2=-1$. Likewise, the sequence $\dots11111111_2=-1$, $\dots11111110_2=-2$, $\dots11111100_2=-4$, etc., despite becoming more and more negative, approaches $0$.
Finally, with this intuition hopefully, solidified we may define negative finite ordinals by the $$\forall n\in \Z (-n := \omega - n),$$ where $\omega=\{0,1,2,\dots\}$ and $A-B$ is the set difference. That is to say, $$\begin{align*} &\vdots\\ -3 &= \{3,4,5,\dots\}\\ -2 &= \{2,3,4,\dots\}\\ -1 &= \{1,2,3,\dots\}\\ 0 &= \emptyset\\ 1 &= \{0\}\\ 2 &= \{0,1\}\\ 3 &= \{0,1,2\}\\ &\vdots \end{align*}$$ i.e; the negatives are compliments to the positives, relative to $\omega$. This definition fulfills several properties previously discussed in the above section on set theory. For instance, for any $m,n\in\Z^-$, the properties If we may recall, these were the properties which would have to have been broken for any definition of integers, so it is convenient that they are still obeyed internally within the negatives, at least. However, of course, they generally do not hold for all integers. Furthermore, it is clear that $-(-n)=n$, so double negation is satisfied. We also get the additional property that $n\cup(-n)=\omega$ for all integers $n$, so $\omega$ acts something like an identity element, like zero, despite not being any integer itself. Actually, by our definition, $-0=\omega$, so by equality we unfortunately must have to either mean something different from that set up by extensionality, or make an exception for $0$. Indeed, since all negative ordinals, by this definition, have the same (countably infinite) cardinality, we must distinguish integers a little more carefully. Fortunately, the remedy is simple. Therefore, any set $X\subseteq \omega$, for example, such that $|\omega-X|=n$ for any $n\in\N$ would be considered equivalent to $-n$.

Applying this definition

By our definition, $\R^{-n}$, for some $n\in\N$ must be equivalent to $\R^{\omega-n}$. Therefore, negative dimensional spaces are infinite-dimensional. For instance, a point $(x_1,x_2,\dots)\in\R^{-1}$ is a tuple with indices $i\in(-1)=\{1,2,\dots\}$. Similarly, a point $(x_2,x_3,\dots)\in\R^{-2}$ is a tuple with indices $i\in(-2)=\{2,3,\dots\}$. Hence, $$\cdots\R^{-3}\subseteq \R^{-2} \subseteq \R^{-1}.$$ However, by the equivalence of cardinality of the negatives, we also have $$\R^{-m}\cong \R^{-n},$$ for any $m,n\in\N$, so the difference between any two spaces of negative dimension is extremely subtle. One may point out that we do not have the property that $\R^n\times\R^{-n}\cong \R^0$, however this was never a property to begin with, since the coproduct in the category of sets is disjoint union, which, as already mentioned, cannot serve as a definition for addition over the integers without the existence of negative cardinals. So, what we actually have is that $A^B\times A^C\cong A^{B\sqcup C}$.

Negative fractal dimension

There is already several notions of non-natural number dimensions for instance, in that of Hausdorff dimension, Similarity dimension, and Box counting dimension, to name a few. In many cases, two or more of these measures are equivalent, but there are cases where they differ. In regard to similarity dimension, loosely speaking, if a fractal is a union of $b$ copies of itself, each scaled by a factor of $a^{-1}$, then it has a similarity dimension of $\log_b(a)$. For instance, the Sierpinski triangle can be thought of as containing 3 copies of itself scaled by a factor of $\frac{1}{2}$, hence having similarity dimension of $\log_3(2)\approx 1.58$[6][6] This may also be thought of as something of a measure of the degrees of freedom of a point "living" in it.. In this case, all three of the aforementioned dimension fot the Sierpinski triangle agree. In any case, should this notion hold more generally, if there exists a shape which is the union of 2 copies of itself, each scaled by a factor of 2, then this measure $\log_b(a)$ is precisely $-1$. Intuitively, no shape of finite measure can have this property. At present, it is unclear if such a shape exists.

Attempts towards the existence of a trivial example

We may nevertheless speculate about a trivial example embedded in $\N$.
Does there exist some $C\subseteq \N$, s.t. there exists $A,B\subseteq C$ s.t. I.e; $C$ is the union of two copies of itself, $A$ and $B$, each scaled by a factor of $2$ and shifted by $k_A$ and $k_B$ respectively. It is not so difficult to show that for any $n\in C$, we must also have $2^k n + \alpha k_A+\left(2^k-1-\alpha\right) k_B\in C$, for any $k\in\N$ and $\alpha\in\N$, s.t. $\alpha\le 2^k-1$. Hence, we may interpret $n$ as "seed" for the set, and $k_A$ and $k_B$ as that which generates the rest of the elements. Without loss of generality, we may assume $0\in C$, and $k_A\lt k_B$ and take the case that $n=0$. Hence, It appears that for some values of $k_A$ and $k_B$, these criteria are almost sufficient.
$$\text{Graph 3. Interactive graph of $C$ as a union of $A$ and $B$.}$$ We encourage the reader to play around with the above graph, where the orange, blue and purple tiles represent $A$, $B$ and $C$, respectively (being cautious to avoid values of $k_A$ and $k_B$ which cause overlap), to demonstrate for themselves that when $A\cap B=\emptyset$, then $A\cup B=C\setminus\{0\}$. I.e; notice that the orange and blue sets are scaled and translated copies of the purple set, which is the union of them both, and zero.

Research by Mandelbrot and Frame

Benoit B. Mandelbrot and Michael Frame, in their paper, A Primer of Negative Test Dimensions and Degrees of Emptiness of Latent Sets, explored the topic of negative dimensions in several ways. We highlight some of their research here.

Intersection formula

There does exist a formula concerning the dimension of the intersection of some spaces which does exhibit negative results. In general, $$\mathbb{S}\in\mathcal{P}(\R^n)\implies \text{dim}\left(\bigcap_{X\in\mathbb{S}}X\right)=n-\sum_{X\in\mathbb{S}}(n-\text{dim}(X)).$$ Or in plain language, for any family $\mathbb{S}$ of spaces that are, each, a subset of $\R^n$, the dimension of their intersection is given by the difference between $n$ and the sum of their differences of $n$ and their dimension. For instance, in $\R^3$, a plane has a dimension of $2$, and an intersection of two of them is typically a line of dimension $1$. This is illustrated by the above formula, which yields $$\text{dim}(X_1\cap X_2)=3-(3-\text{dim}(X_1))-(3-\text{dim}(X_2))=3-(3-2)-(3-2)=1,$$ for planes $X_1$ and $X_2$. However, by the same, formula, if instead $X_1$ and $X_2$ are lines in $\R^3$, then the dimension of their intersection is $$\text{dim}(X_1\cap X_2)=3-(3-\text{dim}(X_1))-(3-\text{dim}(X_2))=3-(3-1)-(3-1)={\color{red}-1}.$$ This, by itself, is not so surprising, for the intersection of two lines in $\mathbb{R}^3$ is typically empty. As such, it is commonly interpreted that an empty set has dimension $-1$. However, there appears to be various degrees of emptiness, as per the title of their paper. For instance, the intersection of $|\mathbb{S}|=k$ lines in $\R^3$ has dimension $$\text{dim}\left(\bigcap_{X\in\mathbb{S}}X\right)=3-\sum_{X\in\mathbb{S}}(3-\text{dim}(X))=3-\sum_{X\in\mathbb{S}}(3-1).=3-2|\mathbb{S}|=3-2k,$$ which becomes increasingly negative with respect to $k$.

Articles referencing here